in FDM 3D printing temperature signature and evolution are some of the main contributors to bonding, which eventually defines shape, distortion, and mechanical properties. We want to analytically study the sensitivity of the filament temperature to some of the main variables in the list of selected process parameters, such as filament diameter, envelope temperature, and printing speed.
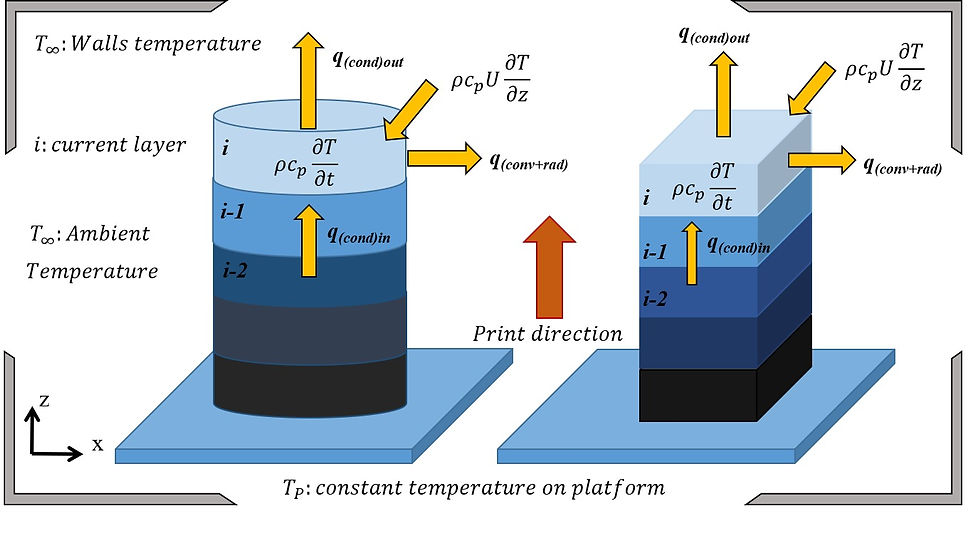
None-dimensionalization can provide an extendable understanding of the effects of some of the parameters. Thus, we revisited the transient thermal heat transfer for 1D ODE as shown here:
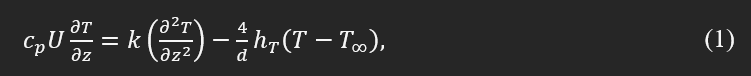
and we introduced the following none-dimensionalized terms to define a new ODE:
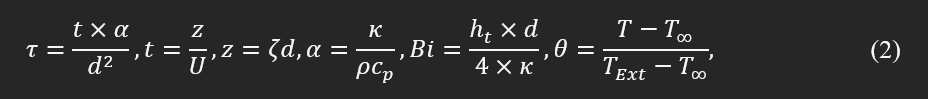
τ is non-dimensionalized time, ζ is non-dimensionalized length, θ is non-dimensionalized temperature, and finally α is non-dimensionalized conductivity as one may interpret them. It is worth noting that z, which can be defined based on extruder motion or a slender part deposition direction, indicates the axis of 1D analyses.
One can rewrite the Eq. (1) in the following non-dimensionalized form:
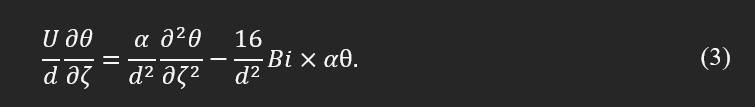
We solved Eq. (3) for a filament leaving an extruder with the area equal to the area of a nominal size of the extruder. In this case, z-axis is along the relative direction of the extruder with U indicating the speed. We assume the coordinates are attached to the extruder and move with it. We also speculate that the filament leaves the extruder in temperature equal to the extruder temperature. L is the deposited length at time t, and by applying the following boundary conditions, one can obtain non-dimensional temperature distribution, θ, as:
With θ1=0 at ζ=0 and 0<= t <=L/U
And θ0=0 , at ζ=inf and 0<= t <=L/U
where,
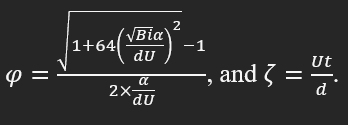
We define a critical length, Lc, the length to which the temperature of the filaments falls under the glass transition temperature, Tg,
where,
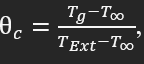
and is Tg glass transition temperature. We found Lc as:
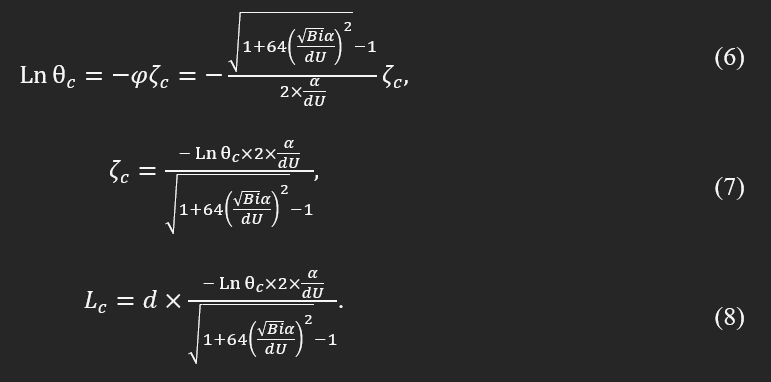
Equation (6) gives the non-dimensional critical length, ζc, from which the critical length, Lc, is obtained. We estimated the critical length and critical time for different configurations. Before, we first estimated the coefficient of convection heat transfer, hconv., and Biot number, as listed in Table 1.
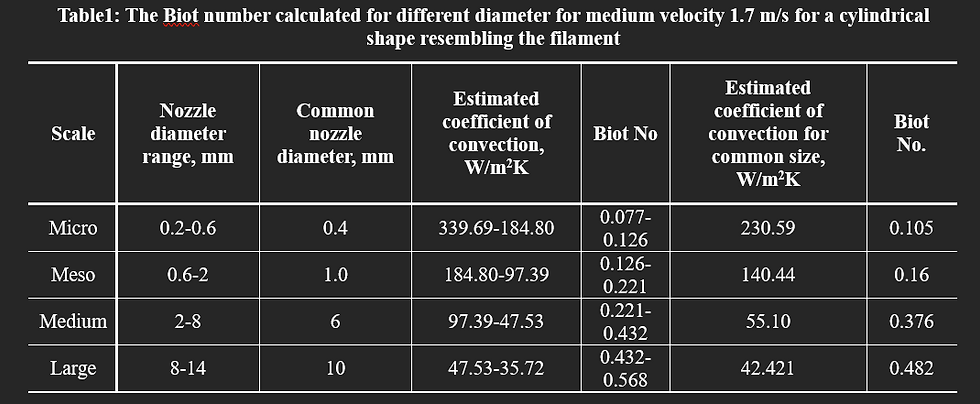
The range of the Biot number indicates that the assumption of lumped-capacity may marginally apply to “Micro” and “Small” cases but not to “Medium” and “Large” cases because Biot No. is more than 0.1. Nonetheless, the lumped-capacity assumption is extended to the latter two cases as well.
In theory, the period a filament stays above the glass transition temperature defines the bonding potential and bonding quality. Thus, we find the period that filament is kept above the critical temperature:
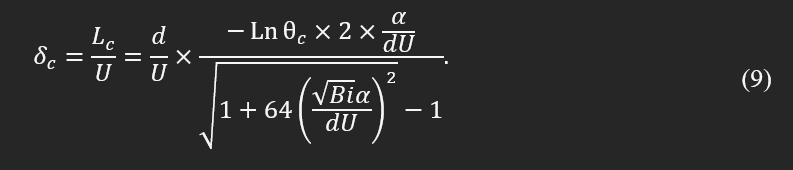
Looking into the critical time, δc, and substituting approximate values for the inside of the square root indicates that the values for (64xBixα^2)/(d^2xU^2) are small in comparison to 1. So based on the Taylor's series, the square root can be approximated by the first order in the following fashion:
If assume,
then:
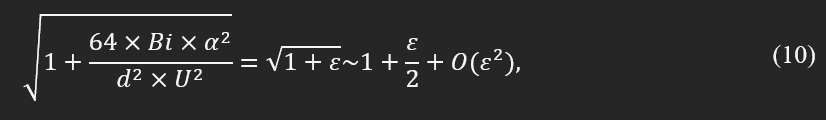
thus,
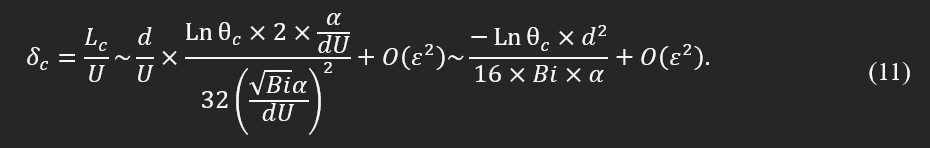
The final equation indicates that the speed of printing does not have a significant effect on the critical time, which is more affected by the size, the coefficient of thermal convection, and material properties. Looking more closely at the equation and substituting Bi and α reveals that there is a linear relationship between density and diameter and a reverse relation to the coefficient of thermal convection.
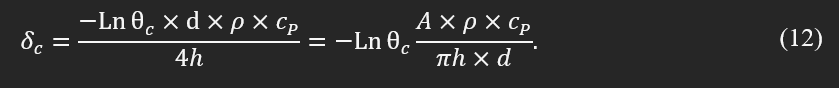
This observation can be physically interpreted as the energy added to the material due to the volumetric flow over the energy being dissipated by convection. It can be noted that conduction does not play a role in the critical time, and one may attribute this independency to its small magnitude in the polymers; thus, temperature distribution relates to the size of the nozzle and the heat transfer coefficient. Other variables—including deposition velocity, raster angle, and air gap—seem less capable of affecting temperature distribution; therefore, the bonding in intra- or inter-layers depends on material properties, diameter, enveloped temperature, and cooling rate.
The effect of diameter and layer thickness is more pronounced in large 3D printers than smaller ones because the size of the nozzles significantly affects the coefficient of thermal convection. For example, when the nozzle size increases from 0.4 mm to 10 mm, hconv becomes five times smaller (decreases from 230.59 to 42.42 W/m2K).
Table 2 shows the calculated sensitivity of the critical time based on Eq. (12) for nominal values associated with the average of common polymeric material properties listed here.
The diameter is based on the nominal diameter of each category, and the convection heat coefficient corresponds to that nominal size as itemized in Table 1.
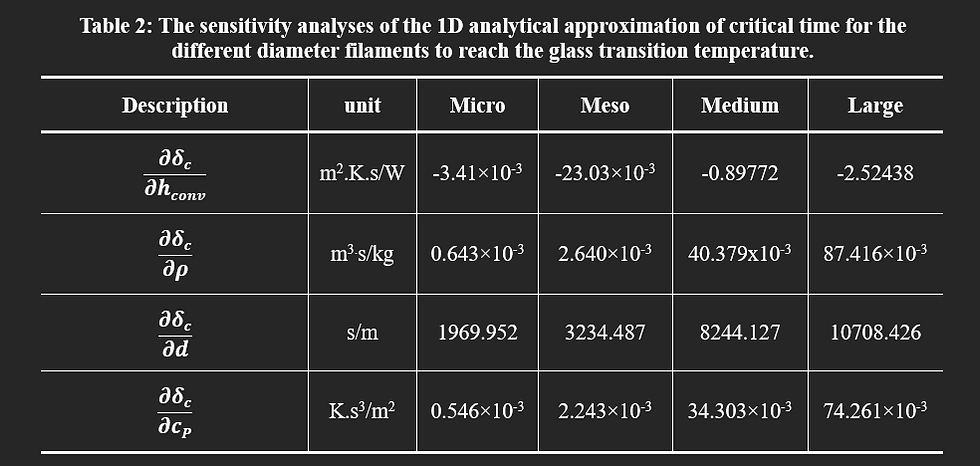
Further analyses on the sensitivity of the critical time to these four variables (d, ρ, Cp, and hconv) shows that, among these variables, the sensitivity to diameter is by far the most pronounced and intensifies as the size of the printer increases. Furthermore, the sensitivity to heat convection is more important for critical time than density and specific heat capacity. The two latter are almost equally unimportant, and their effect may be ignored at the critical time. From this perspective, it can be concluded that the most critical parameters in terms of defining the quality of bonding between layers are nozzle diameter, part size, and cooling rate. Since the nozzle diameter directly defines the thickness and the dimension of the bead, these two factors inherently influence the bonding in inter- and intra-layers and subsequently strength and mechanical properties. In summary, critically important variables are nozzle diameter, enveloped temperature, cooling rate, and the diameter and size of the bead and part.
The changes in the critical time for four cases of different diameters, as explained in Table 1, are shown in Fig. 1 for changes in density, specific heat capacity, and dimensionless temperature.
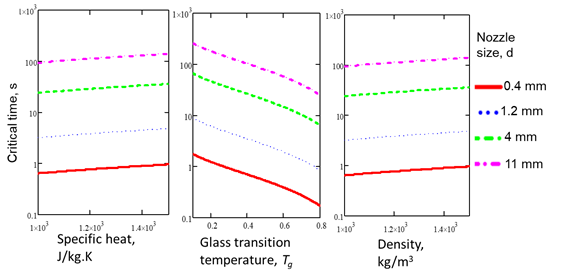
Fig 1. The critical time changes for different nozzle sizes and associated convection heat transfer coefficients as tabulated in Table 1 for density, specific heat capacity, and dimensionless glass transition temperature.
It also has to be taken into consideration that increasing the diameter from 0.4 mm, which is a standard size for the majority of the desktop 3D printers, to 1 mm increased the critical time up to 4 times from 0.78 s to 3.21 s .
It is also worth noticing that the Biot number is not below 0.1 for the third and fourth rows, and the perimeter of the filament decreases in temperature faster than the middle. This temperature distribution from the perimeter toward the center affects the reliability of this approximation for the nozzle with diameters larger than 2 mm. However, this uneven distribution is not detrimental, as explained in the following chapter.
As illustrated in Fig. 2, critical time is nearly flat for different sizes of the filament as the extrusion deposition speed changes from 1000 mm/min to 18,000 mm/min. These graphs are obtained using the original formulation, as expressed in Eq. (9) before applying simplification.
Fig 2. The critical time changes for different standard nozzle sizes and associated convection heat transfer coefficients as tabulated in Table 1 for different deposition linear velocities range from 1000 mm/min to 18,000 mm/min (0.017to 0.3 m/s).
References:
[1] Pooladvand, K., 2019, "Multifunctional Testing Artifacts for Evaluation of 3d Printed Components by Fused Deposition Modeling," Worcester Polytechnic Institute, [Link].
Comentarios